Introduction
With the significant increase in the amount of available information on the internet, the demand for a reliable recommender system has grown rapidly. Among different variations, sequential recommendation typically aims at predicting the most probable next item that a certain user would be interested in given previous interaction history. In the era of advanced neural networks, diverse approaches to sequential recommendation have shown improved performance by adopting enhanced model architectures such as Transformers and graph neural networks [3]. In terms of training objectives, however, comparably fewer approaches have been introduced. Specifically, most approaches still adhere to either pointwise (BCE) loss [1, 2] or pairwise (BPR) loss [4, 5], respectively. In this work, we thus introduce a new training objective that enhances the recommendation performance by adopting normalized embeddings.
Sequential Recommendation
Below, we provide basic formulation of the sequential recommendation problem. Let a set of \(M\) users be \(\mathcal{U} = \{u_1, \ldots, u_M\}\) and a set of \(N\) items be \(\mathcal{I} = \{i_1, \ldots, i_N\}\). A sequential recommendation task requires capturing a dynamic user behavior from a previous interaction history. By utilizing the previous interaction history of a user \(u\), denoted as \(h_u = \{i_1^u, \ldots, i_t^u\}\), where \(i_j^u\) is \(j\)th item for \(u\) and eventually \(i_1^u, \ldots, i_t^u\) are chronologically ordered, a goal of sequential recommendation is to select the most relevant next item \(i_{t+1}^u \in \mathcal{I}\) to \(u\).
Given a history \(h_u\) and an item \(i_k\), a model, parameterized by \(\boldsymbol \theta\), first projects \(h_u\) and \(i_k\) onto the vectors of the same dimension \(h'_u\) and \(i'k\), respectively. Then, a recommendation score \(\hat{s}_{uk}\) between \(h'_u\) and \(i'_k\) is calculated through an inner product of the two vectors as \({h'_u}^\top i'_k\).
Normalization
In a variety of applications including computer vision and natural language processing [7, 8], the use of normalized representation is a de facto standard due to its proven effectiveness and robustness. In a typical sequential recommendation scenario, we can naively adopt normalization to both history and item embedding.
\begin{equation} \bar{h}'_u = \frac{h'_u}{\|h'_u\|_2} \quad \textrm{and} \quad \bar{i}'_k = \frac{i'_k}{\|i'_k\|_2}. \end{equation}
To validate its effectiveness, we report the resulting recommendation performance by comparing the use of unnormalized embeddings to the use of normalized embeddings where a neural architecture and loss are fixed.
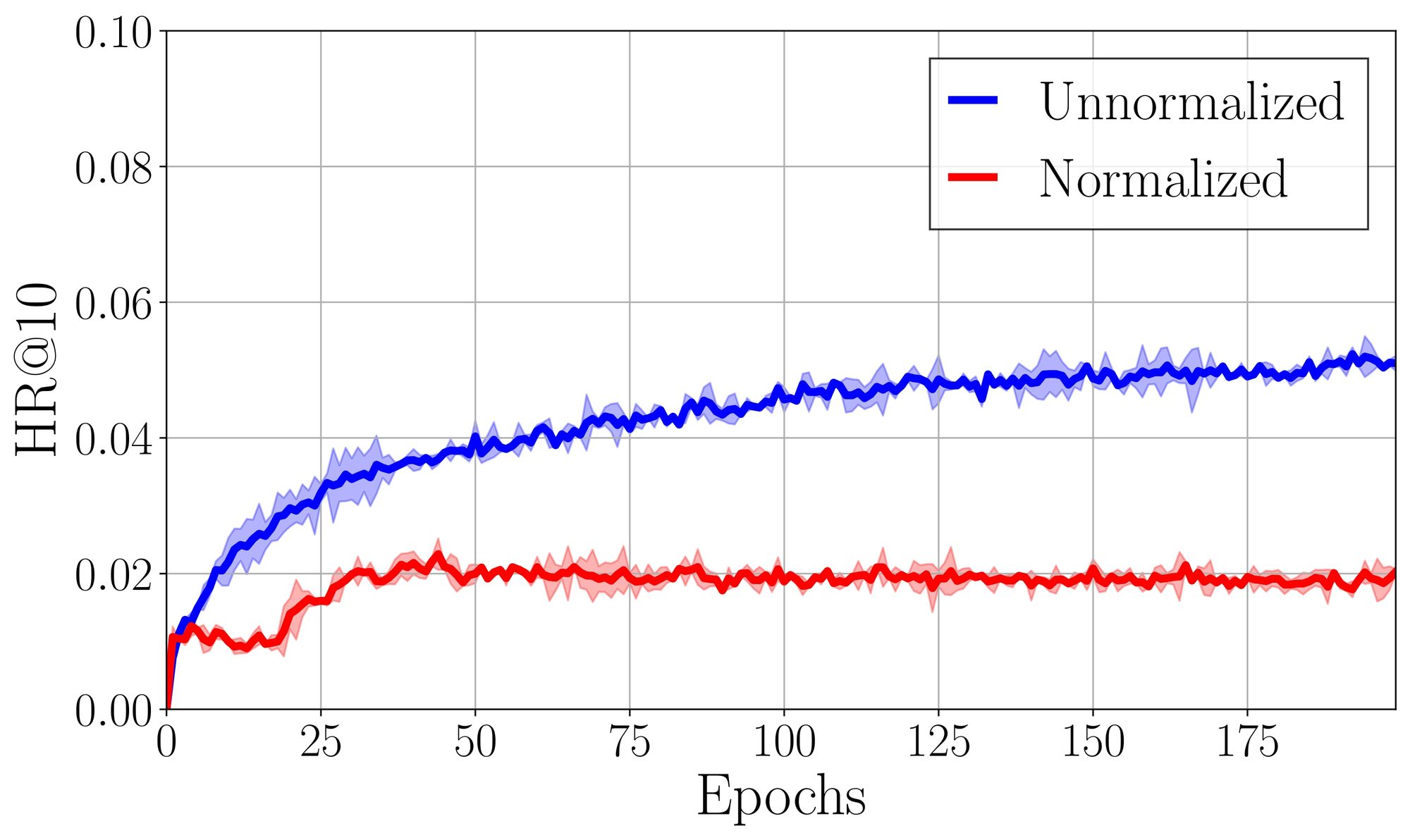
Surprisingly, We find that the naive adoption of normalization to the training of the recommender system instead leads to a significant performance drop of the recommendation quality. We assume that the normalized representations do not preserve substantial information for recommendation as magnitudes are removed. To validate our hypothesis, we calculate a pairwise cosine similarity of normalized item and history embeddings independently.
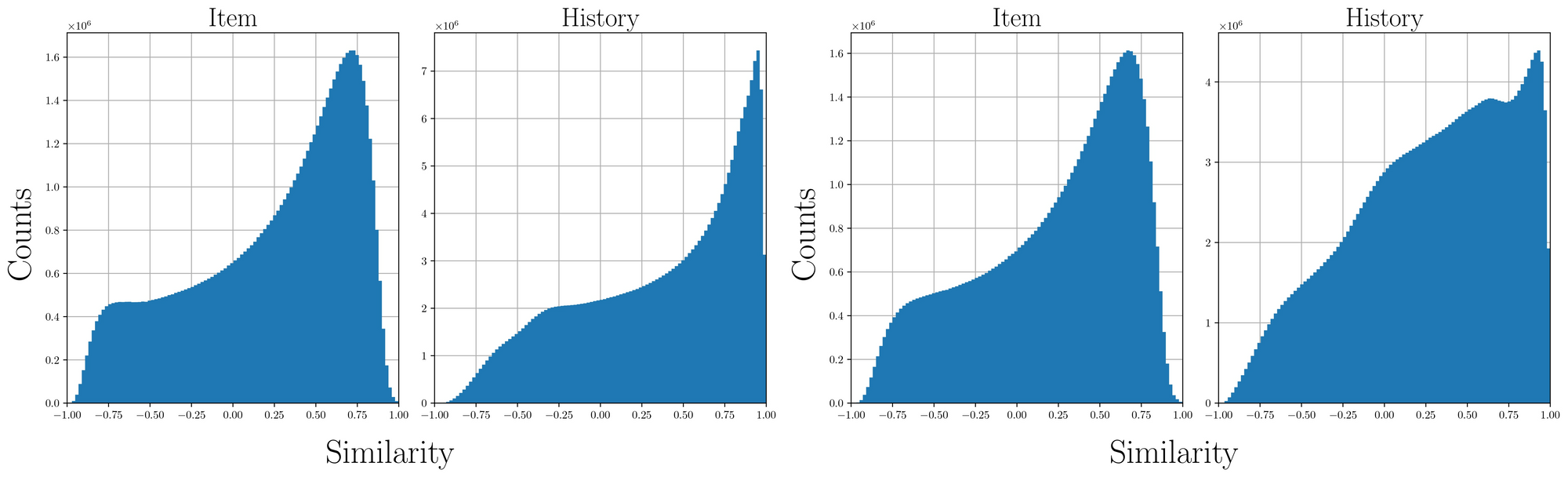
We observe that the history embeddings are typically clusterized at the early stage of the training. While the level of skewness decreases as training proceeds, we still find the bias of embeddings, not covering a broad surface of the unit hypersphere. Nevertheless, we see that performance slowly increases as embeddings become less biased which is consistent with our hypothesis.
Proposed Method
To preserve maximal information with normalized information, we need to develop training objectives that prevent the clusterization of embeddings. Thus, we present a novel training objective for such purpose and explain rationales behind each term in detail.
While learning effective recommendation policy, our learned embeddings should be distributed evenly as much as possible on the hypersphere thereby preserving sufficient information for recommendation. We, therefore, design two regularization term based on the Gaussian potential kernel [6] over embeddings but with a slight modification.
Given a batch of \((u, i, j)\), we split into two disjoint sets: \(\mathcal{D}_H\) consisting of only history embeddings and \(\mathcal{D}_I\) consisting of only item embeddings. We then calculate a sum of pairwise Gaussian potentials for each set homogeneously:
\begin{equation} \mathcal{L}_\textrm{hom} = \sum_{x, y \in\mathcal{D}_H} e^{-t \|\bar{h}'_x - \bar{h}'_y\|_2^2} + \sum_{x, y \in\mathcal{D}_I} e^{-t \|\bar{i}'_x - \bar{i}'_y\|_2^2} \end{equation}
where \(\bar{h}'\) and \(\bar{i}'\) are normalized history and item embeddings, respectively.
Similarly, we define a heterogeneous term as a sum of pairwise Gaussian potentials between each history and negative item embedding:
\begin{equation} \mathcal{L}_\textrm{het} = \sum_{x \in\mathcal{D}_H, y \in\mathcal{D}_J} e^{-t \|\bar{h}'_x - \bar{i}'_y\|_2^2} \end{equation}
where \(\mathcal{D}_J\) is a subset of \(\mathcal{D}_I\), containing only negative items from the batch.
For recommendation loss, we adopt pairwise (BCE) term such that:
\begin{equation} \mathcal{L}_\textrm{rec}(\mathcal{D}; \boldsymbol\theta) = - \sum_{(u,i,j) \in\mathcal{D}}\log\sigma(\hat{s}_{ui}; \boldsymbol\theta) + \log (1 - \sigma(\hat{s}_{uj}; \boldsymbol\theta))\end{equation}
Combining three terms, our final loss is:
\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{rec} + \beta_{1}\mathcal{L}_\textrm{hom} + \beta_{2}\mathcal{L}_\textrm{het}. \end{equation}
For simplicity, we set the regularization hyperparameters \(\beta_1\), and \(\beta_2\) to same value of \(\beta\).
Experiments
We use four public sequential recommendation benchmarks: Beauty, Toys, and Sports categories from the Amazon datasets and the Yelp dataset. With the trained model, we recommend \(K\) items with the highest scores from the entire item pool. To evaluate the quality of a trained recommendation model, we adopt two common top-\(K\) metrics: top-\(K\) Hit Ratio (HR@\(K\)) and top-\(K\) Normalized Discounted Cumulative Gain (NDCG@\(K\)). For simplicity, we set \(K\) fixed to the value of 10.
We verify the effectiveness of our proposed loss with three different architectures for embedding backbones; GRU4Rec, Caser, and SASRec. Within each architecture, we only switch the training objective between, BCE, BPR, InfoNCE, and our loss; then measure the quality of the learned recommendation policy for valid comparisons.
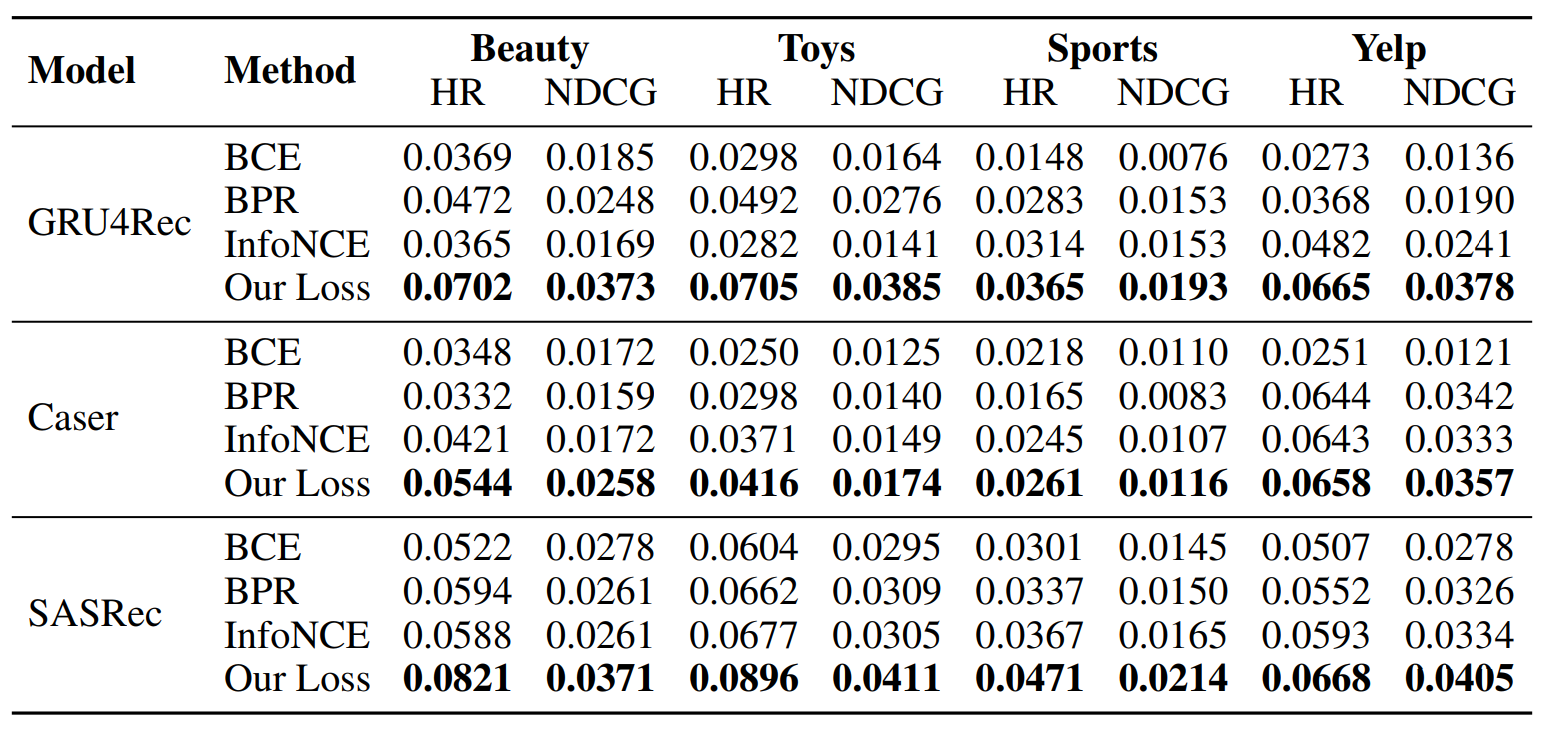
We observe that our proposed objective consistently outperforms all baseline methods regardless of the embedding architectures. Such results imply that a model with normalized embeddings can exhibit improved quality in recommendation when properly trained. Specifically, we presume that our method successfully resolves the aforementioned clusterization issue of the embeddings when naively adopting embedding normalization.
Summary
In this work, we focused on applying embedding normalization to the training process of recommender systems. We analyzed the possible cause of performance drop with simple adoption of embedding normalization. To tackle the issue, we proposed a novel uniformity-inspired objective that enhances the quality of recommendation with normalization. Our work has been presented in Self-supervised Learning: Theory and Practice workshop at NeurIPS 2023 (SSL-PT). More details can be found in the presented paper.
Reference
[1] Jianxin Chang, Chen Gao, Yu Zheng, Yiqun Hui, Yanan Niu, Yang Song, Depeng Jin, and Yong Li. Sequential recommendation with graph neural networks. In Proceedings of the ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), pages 378–387, Virtual, 2021. ACM.
[2] Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. Neural collaborative filtering. In Proceedings of the Web Conference (WWW), pages 173–182, Perth, Australia, 2017. ACM.
[3] Thomas N Kipf and Max Welling. Semi-supervised classification with graph convolutional networks. In Proceedings of the International Conference on Learning Representations (ICLR), Palais des Congrès Neptune, Toulon, France, 2018. OpenReview
[4] Steffen Rendle and Christoph Freudenthaler. Improving pairwise learning for item recommendation from implicit feedback. In Proceedings of the IEEE International Conference on Data Mining (ICDM), pages 273–282, Shenzhen, China, 2014. IEEE.
[5] Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the Conference on Uncertainty in Artificial Intelligence (UAI), pages 452–461, Montreal, Quebec, Canada, 2009. AUAI Press.
[6] Tongzhou Wang and Phillip Isola. Understanding contrastive representation learning through alignment and uniformity on the hypersphere. In Proceedings of the International Conference on Machine Learning (ICML), pages 9929–9939, Virtual, 2020. JMLR.
[7] Feng Wang, Xiang Xiang, Jian Cheng, and Alan Loddon Yuille. Normface: L2 hypersphere embedding for face verification. In Proceedings of the ACM International Conference on Multimedia (MM), pages 1041–1049, New York, New York, USA, 2017. ACM.
[8] Zhirong Wu, Yuanjun Xiong, Stella X Yu, and Dahua Lin. Unsupervised feature learning via non-parametric instance discrimination. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), pages 3733–3742, Salt Lake City, Utah, USA, 2018. IEEE




