Introduction
Sequential recommendation, nowadays, plays an indispensable role in numerous e-commerce applications to appropriately predict and match each user's potential needs. Conventional deep learning-based approaches [1, 2] formulates this task as learning the feature representations of a history of a user's previously interacted item and a candidate (i.e, unobserved) item. Here, a vast majority of models adopt one of three training objectives: 1) pairwise (e.g, BPR [3]), 2) pointwise (e.g, BCE [4]), and 3) setwise (e.g, SSM [5]) losses. While effective, there exists a shared downside of regarding all unobserved items equally negative. To mitigate this issue, we propose a novel method that extends original objectives such that different degrees of preferences of unobserved items are reflected to their recommendation scores.
Sequential Recommendation
Below, we provide basic formulation of the sequential recommendation problem. Let \(\mathcal{U} = \{u_1, \ldots, u_M\}\) and \(\mathcal{I} = \{i_1, \ldots, i_N\}\) denote sets of \(M\) users and \(N\) items, respectively. Given a previous interaction history of a user \(u\) as \(h_u = \{i_1^u, \ldots, i_t^u\}\), the goal of a sequential recommendation model is to select and recommend a next item \(i_{t+1}^u\) that is most likely to be relevant to the user \(u\). Typically, we map the history a history \(h_u\) and an item \(i_k\) to latent representations of \(h'_u\) and \(i'k\), respectively. Then, a recommendation score \(\hat{s}_{uk}\) between \(h'_u\) and \(i'_k\) is calculated through an inner product of the two vectors as \({h'_u}^\top i'_k\).
Training Objectives
Pairwise Objective. Bayesian personalized ranking (BPR) [3] models each user's personalized ranking of candidate items. It ensures the recommendation score of the next interacted (i.e., positive) item to be higher than scores of the rest unobserved (i.e., negative) items. Thus with a dataset \(\mathcal{D}_s\) of triplets \((u,i,j)\) where the item \(i\) is a positive and \(j\) is a sampled negative to the user \(u\), the loss is formulated as:
\begin{equation} \mathcal{L}_{\textrm{BPR}} = -\sum_{(u,i,j) \in \mathcal{D}_s} \log\sigma(\hat{s}_{ui} - \hat{s}_{uj}). \end{equation}
Here, \(\sigma(\cdot)\) is a sigmoid function and the term \(\sigma(\hat{s}_{ui} - \hat{s}_{uj})\) is a probability of the user \(u\) preferring the positive \(i\) more than the sampled negative \(j\).
Pointwise Objective. Binary cross-entropy (BCE) [4] reformulates the recommendation problem to a typical binary classification with single sampled negative from unobserved items. With a dataset \(\mathcal{D}_s\), the loss is defined as:
\begin{equation} \mathcal{L}_{\textrm{BCE}} = -\sum_{(u,i,j) \in \mathcal{D}_s} \log\sigma(\hat{s}_{ui}) + \log(1 - \sigma(\hat{s}_{uj})). \end{equation}
Setwise Objective. Sampled softmax loss (SSM) [5] turns the recommendation problem into a multi-class classification with a fixed-size set of sampled negatives. With a dataset \(\mathcal{D}_m\) consisted of a triplet \((u, i, \mathcal{N}_j)\) where \(\mathcal{N}_j\) is a sampled set of negatives to the user \(u\), the loss is formulated as follow:
\begin{equation} \mathcal{L}_{\textrm{SSM}} = -\sum_{(u,i,\mathcal{N}_j) \in \mathcal{D}_m} \log\frac{\exp(\hat{s}_{ui})}{\exp(\hat{s}_{ui}) + \sum_{j \in \mathcal{N}_j}\exp(\hat{s}_{uj})}. \end{equation}
Weak Transitivity
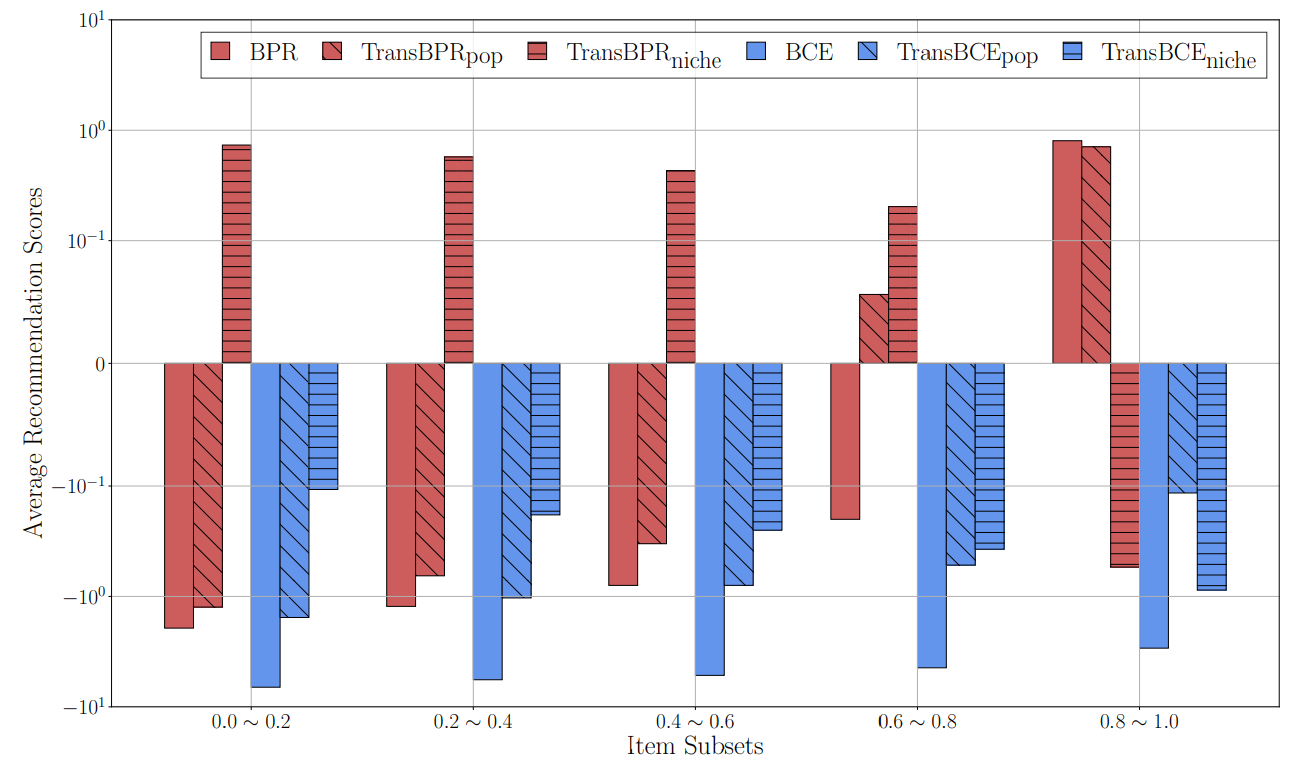
Inducing orders on recommendation scores of unobserved items requires a model to sample two or more negatives differing in preferences. Let \(p_1\) and \(p_2\) represent two different sampling distributions for negatives. Given a user \(u\) and the positive item \(i\), we then obtain a negative \(j\) from \(p_1\) and \(k\) from \(p_2\). Transitivity is a trifold relation of \(\hat{s}_{ui} > \hat{s}_{uj} > \hat{s}_{uk}\) where the negative \(j\) is less preferred than the positive \(i\) while more preferred than the other negative \(k\). Strict transitivty then corresponds to a scheme where any \(j\) is guaranteed to be more preferred than any \(k\). Weak transitivity, on the other hand, allows occasional violations of the relation such that \(j\) might be less preferred than \(k\). For a set of sampled negatives, we slightly modify the relation. Let \(\mathcal{N}_j = {j_1, \ldots, j_n}\) a set of negatives from \(p_1\) and \(\mathcal{N}_k = {k_1, \ldots, k_n}\) a set of negatives from \(p_2\), the transitive relation is modified as \(\hat{s}_{ui} > \max(\hat{s}_{\mathcal{N}_j}) > \min(\hat{s}_{\mathcal{N}_j}) > \max(\hat{s}_{\mathcal{N}_k})\) where \(\hat{s}_{\mathcal{N}_j} = \{\hat{s}_{uj_1}, \ldots, \hat{s}_{uj_n}\}\) and \(\hat{s}_{\mathcal{N}_k} = \{\hat{s}_{uk_1}, \ldots, \hat{s}_{uk_n}\}\).
Loss Extensions
We propose novel extensions of original recommendation objectives. By utilizing an item popularity distribution \(p_\textrm{pop}\) and a uniform distribution \(p_\textrm{unif}\), we introduce two sampling methods that incorporate the previously stated weak transitivity.
\begin{align} \mathcal{D}'_{s}(\textrm{pop})=\{(u,i,j,k) \mid j \sim p_\textrm{pop}, k \sim p_\textrm{unif}\} \\ \mathcal{D}_{s}(\textrm{niche})=\{(u,i,j,k) \mid j \sim p_\textrm{unif}, k \sim p_\textrm{pop}\} \end{align}
Here, we refer \(j\) as more preferred negative whereas \(k\) as less preferred negative. Therefore, the generated mini-batch \(\mathcal{D}_{s}(\textrm{pop})\) assumes a user generally preferres popular items while \(\mathcal{D}_{s}(\textrm{niche})\) regards niche (i.e., less popular) items more favored.
Our BPR loss extension with weak transitivity is then defined as below:
\begin{equation}\mathcal{L}_{\textrm{TransBPR}}=-\sum_{(u,i,j,k)\in\mathcal{D}'_{s}}\underbrace{\textrm{log}\sigma(\hat{s}_{ui}-\hat{s}_{uj})}_{\textrm{original}}+\gamma\underbrace{\textrm{log}\sigma(\hat{s}_{uj}-\hat{s}_{uk})}_{\textrm{preference}},\end{equation}
where \(\gamma\) is a coefficient that balances the original term and the preference term. While the original term assures the score of more preferred negative to be smaller than that of the positive, the preference term encourages it to be higher than the score of less preferred negative. Thus, our extension imposes the transitive relation \(\hat{s}_{ui} > \hat{s}_{uj} > \hat{s}_{uk}\) to learned scores.
By combining the proposed loss formulation with previously introduced sampling methods, we obtain two training objectives.
\begin{align}\textrm{TransBPR}_\textrm{pop} &= \mathcal{L}_{\textrm{TransBPR}}(\mathcal{D}'_{s}(\textrm{pop});\theta) \\ \textrm{TransBPR}_\textrm{niche} &=\mathcal{L}_{\textrm{TransBPR}}(\mathcal{D}'_{s}(\textrm{niche});\theta),\end{align}
where \(\theta\) is learnable parameters of the recommendation model.
Similar to BPR extensions, BCE loss function can be extended as follows:
\begin{equation}\mathcal{L}_{\textrm{TransBCE}}=-\sum_{(u,i,j,k)\in\mathcal{D}'_{s}}\Bigl[\textrm{log}(\sigma(\hat{s}_{ui})) + \textrm{log}(1 - \sigma(\hat{s}_{uj})) + \gamma\Bigl(\textrm{log}(\sigma(\hat{s}_{uj})) + \textrm{log}(1 - \sigma(\hat{s}_{uk}))\Bigl)\Bigl].\end{equation}
Also, we then combine the proposed formulation with two quadruplet sampling methods to introduce new training objectives which as:
\begin{align}\textrm{TransBCE}_\textrm{pop} &= \mathcal{L}_{\textrm{TransBCE}}(\mathcal{D}'_{s}(\textrm{pop});\theta) \\ \textrm{TransBCE}_\textrm{niche} &=\mathcal{L}_{\textrm{TransBCE}}(\mathcal{D}'_{s}(\textrm{niche});\theta).\end{align}
Setwise losses, on the other hand, require multiple negatives. Therefore, we modify the sampling methods such that we instead sample a set of items \(\mathcal{N}_{j}\) and \(\mathcal{N}_{k}\) from each sampling distribution. Corresponding sampling schemes are defined as below:
\begin{align}\mathcal{D}'_{m}(\textrm{pop})=\{(u,i,\mathcal{N}_{j},\mathcal{N}_{k}) \mid \mathcal{N}_{j} \sim p_\textrm{pop}, \mathcal{N}_{k} \sim p_\textrm{unif}\} \\ \mathcal{D}_{m}(\textrm{niche})=\{(u,i,\mathcal{N}_{j},\mathcal{N}_{k}) \mid \mathcal{N}_{j} \sim p_\textrm{unif}, \mathcal{N}_{k} \sim p_\textrm{pop}\}. \end{align}
Moreover, the extension of SSM loss function is given by:
\begin{equation}\mathcal{L}_{\textrm{TransSSM}}=-\sum_{(u,i,\mathcal{N}_{j},\mathcal{N}_{k})\in\mathcal{D}'_{m} }\Bigl[\textrm{log}\frac{\textrm{exp}(\hat{s}_{ui})}{\textrm{exp}(\hat{s}_{ui}) + \sum_{j\in\mathcal{N}_{j}}\textrm{exp}(\hat{s}_{uj})} + \gamma \frac{1}{|\mathcal{N}_{j}|}\sum_{j\in\mathcal{N}_{j}}\textrm{log}\frac{\textrm{exp}(\hat{s}_{uj})}{\textrm{exp}(\hat{s}_{uj}) + \sum_{k\in\mathcal{N}_{k}}\textrm{exp}(\hat{s}_{uk})}\Bigl]. \end{equation}
By integrating the above formulation with our proposed multiple negative sampling schemes we have our extended training objectives as:
\begin{align}\textrm{TransSSM}_\textrm{pop} &= \mathcal{L}_{\textrm{TransSSM}}(\mathcal{D}'_{m}(\textrm{pop});\theta) \\ \textrm{TransSSM}_\textrm{niche} &=\mathcal{L}_{\textrm{TransSSM}}(\mathcal{D}'_{m}(\textrm{niche});\theta).\end{align}
Experiments
We use four public sequential recommendation benchmarks: Beauty, Toys, and Sports datasets from Amazon and the Yelp dataset. For dataset partitioning, we adopt the conventional \(leave-one-out\) strategy [6] to assure the quality of the trained recommender system. After training the model, we recommend \(K\) items with the highest scores from the entire item pool. To evaluate the quality of a trained recommendation model, we adopt two common top-\(K\) metrics: top-\(K\) Hit Ratio (HR@\(K\)) and top-\(K\) Normalized Discounted Cumulative Gain (NDCG@\(K\)). For simplicity, we set \(K\) fixed to the value of 10.
We fix the model architecture to SASRec [6] for the embedding backbone and only switch the training objective. For baselines, we compare our method against \(\textrm{BPR}\), \(\textrm{GBPR}\) [7], \(\textrm{BCE}\), \(\textrm{SSM}\), \(\textrm{InfoNCE}\) [8], \(\textrm{BPR-DNS}\) [9], and \(\textrm{gBCE}\) [10]. For \(\textrm{gBCE}\), we differentiate methods with a single negative and multiple negative sampling as \(\textrm{gBCE}_{1}\) and \(\textrm{gBCE}_{\mathcal{N}}\).
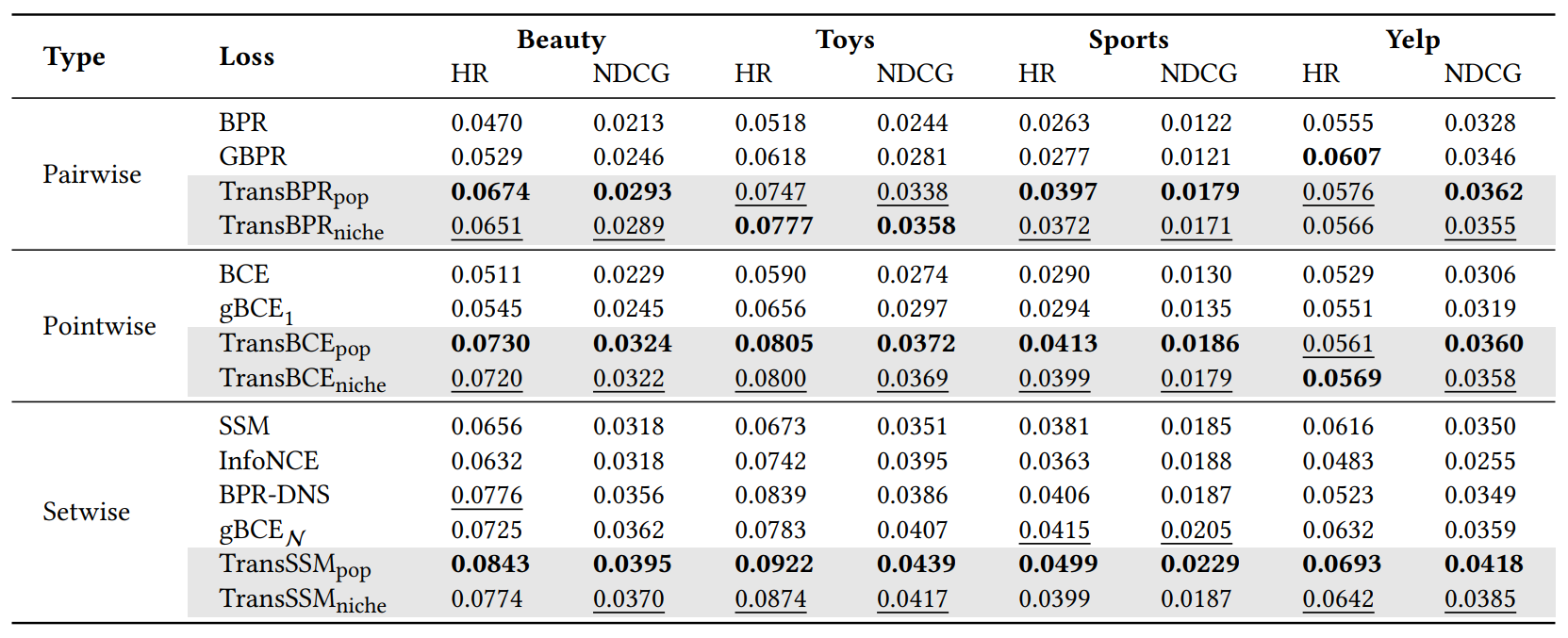
In general, we observe our proposed methods (\(\textrm{TransBPR}\), \(\textrm{TransBCE}\), and \(\textrm{TransSSM}\)) outperform three original objectives (\(\textrm{BPR}\), \(\textrm{BCE}\), and \(\textrm{SSM}\)) and their notable variants. Such results demonstrate that inducing preference order through weak transitivity into the loss functions consistently improves the performance compared to base objectives. Compared to single negative sampling methods, we observe baseline and our extensions with multiple negative sampling typically obtain improved metrics. Specifically, we find favoring more popular items generally effective while niche preference performs on par with best baseline methods often second to the best.
Summary
In this work, we identified a crucial disadvantage of binary label assignments shared within conventional recommendation objectives. To overcome this limitation, we have proposed novel extensions to original objectives that directly exploit the preference differences of unobserved items. Through extensive experiments, we demonstrated the effectiveness of our method compared to baseline methods. Our work will be presented in the Short Research Track of 33rd ACM International Conference on Information and Knowledge Management (CIKM). More details and analysis can be found in the paper.
Reference
[1] Balázs Hidasi, Alexandros Karatzoglou, Linas Baltrunas, and Domonkos Tikk. Session-based recommendations with recurrent neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), San Juan, Puerto Rico, 2016. OpenReview.
[2] Fei Sun, Jun Liu, Jian Wu, Changhua Pei, Xiao Lin, Wenwu Ou, and Peng Jiang. BERT4Rec: Sequential recommendation with bidirectional encoder representations from transformer. In Proceedings of the ACM International Conference on Information and Knowledge Management (CIKM), Beijing, China, 2019. ACM.
[3] Steffen Rendle, Christoph Freudenthaler, Zeno Gantner, and Lars Schmidt-Thieme. BPR: Bayesian personalized ranking from implicit feedback. In Proceedings of the Conference on Uncertainty in Artificial Intelligence (UAI), pages 452–461, Montreal, Quebec, Canada, 2009. AUAI Press.
[4] Xiangnan He, Lizi Liao, Hanwang Zhang, Liqiang Nie, Xia Hu, and Tat-Seng Chua. Neural collaborative filtering. In Proceedings of the Web Conference (WWW), pages 173–182, Perth, Australia, 2017. ACM.
[5] Jiancan Wu, Xiang Wang, Xingyu Gao, Jiawei Chen, Hongcheng Fu, and Tianyu Qiu. On the effectiveness of sampled softmax loss for item recommendation. ACM Transactions on Information Systems 42, 2024.
[6] Wang-Cheng Kang and Julian McAuley. Self-attentive sequential recommendation. In Proceedings of the IEEE International Conference on Data Mining (ICDM), Singapore, Singapore, 2018. IEEE.
[7] Weike Pan and Li Chen. Gbpr: Group preference based bayesian personalized ranking for one-class collaborative filtering. In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 2013. IJCAI.
[8] Aaron van den Oord, Yazhe Li, and Oriol Vinyals. Representation learning with contrastive predictive coding. arXiv preprint arXiv:1807.03748 July (2018).
[9] Weinan Zhang, Tianqi Chen, Jun Wang, and Yong Yu. Optimizing top-n collaborative filtering via dynamic negative item sampling. In Proceedings of the ACM SIGIR Conference on Research and Development in Information Retrieval (SIGIR), Dublin, Ireland, 2013. ACM.
[10] Aleksandr Vladimirovich Petrov and Craig Macdonald. gsasrec: Reducing overconfidence in sequential recommendation trained with negative sampling. In Proceedings of the ACM International Conference on Recommender Systems (RecSys), Singapore, Singapore, 2023. ACM.



